Модуль 2. Общий метод аналитического конструирования нелинейных агрегированных регуляторов
2.1. Направленная самоорганизация и системный синтез
2.1.1. Постановка задачи
Предположим, что поведение системы соответствующей природы может быть отражено следующими дифференциальными уравнениями:
$$
\dot x_i(t) =f_i(x_1,\dots,x_r,y_{r+1},\dots,y_n);
\qquad(2.1)$$ $$
\dot y_j(t) =f_j(x_1,\dots,x_r,y_{r+1},\dots,y_n,u_1,\dots,u_m);
\qquad(2.2)$$
$$i=1,2,\dots,r; \quad j=r+1,r+2,\dots,n; \quad m\le n-r.
$$Это означает, что общая система может быть разбита на подсистему, описываемую “кинематическими” уравнениями (2.1), и подсистему, описываемую “динамическими” уравнениями (2.2), в которых, в отличие от (2.1), присутствуют некоторые функции $u_1,\dots,u_m$ — обратные связи, называемые здесь управлениями. Предположим, что этими функциями мы вправе распорядиться по своему усмотрению и тем самым, в зависимости от нашего желания, “сконструировать” некоторое множество новых систем.
Изложенная здесь ситуация, когда часть системы (“объект управления”) уже задана, а другая часть может быть дополнительно сконструирована, фактически возникает перед конструктором любой современной системы — технической, химико-технологической, энергетической, биоинженерной, экологической и т.д. Учитывая замечательные свойства самоорганизующихся систем различной природы [51, 43, 52, 45, 53, 54], возникает важнейший вопрос о построении искусственных синергетических систем, обладающих в той или иной мере свойствами самоорганизации.
Говоря более конкретно, возникает вопрос о выборе таких функций $u_1,\dots,u_m$ в подсистеме (2.2), чтобы общая макросистема (2.1), (2.2) была бы в той или иной мере самоорганизующейся. Это означает, что применительно к управляемой системе (2.1), (2.2) ставится задача развития такого подхода, когда с помощью обратных связей $u_1,\dots,u_m$ формируются “искусственные” энергетические, технологические, экологические и другие желаемые аттракторы, которые совместно с естественными аттракторами системы (2.1), (2.2) позволяют осуществить направленные процессы самоорганизации в общей макросистеме. Если удастся развить такого рода подход, то тогда появится возможность принципиально расширить области приложения идей синергетики на широчайший класс искусственно создаваемых самоорганизующихся систем нового типа. Оказывается, что такого рода синергетический подход, в принципе, можно развить, опираясь на идеологию и базовые положения синергетической теории управления (СТУ).
2.1.2. Спонтанная самоорганизация и инерциальные многообразия
Для простоты изложения такого подхода рассмотрим сначала известную систему:
$$
\begin{split}
\dot x(t) &=\lambda_1 x -xy;\\
\dot y(t) &=-\lambda_2 y +x^2 +u.
\end{split}
\qquad(2.3)$$
Эта система при $u=0$, т.е.
$$
\begin{split}
\dot x(t) &=\lambda_1 x -xy;\\
\dot y(t) &=-\lambda_2 y +x^2,
\end{split}
\qquad(2.4)$$
использовалась Г. Хакеном [52] для выявления сущности основополагающих понятий синергетики. На основе этих уравнений в [52] описывалось явление спонтанной самоорганизации с бифуркацией типа “вилка”. Если же предположить, что система (2.3) — это искусственно конструируемая система соответствующей физической (химической и др.) природы, то введение в нее функции $u(x,y)$ представляется вполне естественным и оправданным. В [52] показано, что в системе (2.4) при $\lambda_2>>|\lambda_1|$ возникают кооперативные процессы, основанные на адиабатическом приближении $\dot y(t)\approx 0$ и, следовательно, представлении ее движения на финишном этапе известным в синергетике [51, 43, 52, 45, 53, 54] эволюционным уравнением
$$
\dot x(t)\cong\lambda_1 x -\frac 1{\lambda_2}x^3,\qquad
(2.5)$$
записанным относительно параметра порядка $x$. Этому параметру подчинена “быстрая” переменная $y$ в виде уравнения кооперативного состояния
$$
x^2 -\lambda y\cong 0.\qquad
(2.6)$$
Согласно положениям синергетики, уравнение (2.5) имеет точку бифуркации — раздвоения решений при критическом значении ($\lambda_{1c}=0$) управляющего параметра $\lambda_1$. В этой точке в результате действия малых флюктуаций система “принимает” соответствующее решение и дальнейшее ее движение будет происходить по одной из двух равновероятных ветвей асимптотически устойчивого движения, т.е. может возникнуть спонтанная самоорганизация. Описанное необычное явление в синергетике называется бифуркацией типа “вилка”[51, 43, 52, 45, 53, 54].
На рис. 2.1 изображен фазовый портрет системы (2.4) при $\lambda_2/\lambda_1=100$, из которого видно, что траектории сначала устремляются к состоянию (2.6), а затем движутся вдоль него к стационарным точкам $x_s=+\sqrt{\lambda_1\lambda_2}$, $y_s=\lambda_1$ и $x_s=-\sqrt{\lambda_1\lambda_2}$, $y_s=\lambda_1$ соответственно, т.е. имеет место кооперативный процесс. Аналогично, на рис. 2.2 изображен фазовый портрет системы (2.4) при $\lambda_2/\lambda_1=1$, из которого следует, что при таком соотношении параметров $\lambda_1$ и $\lambda_2$ траектории сразу устремляются в окрестность стационарных точек $x_s=\pm\sqrt{\lambda_1\lambda_2}$, $y_s=\lambda_1$, а кооперативные процессы заметно ослабляются.
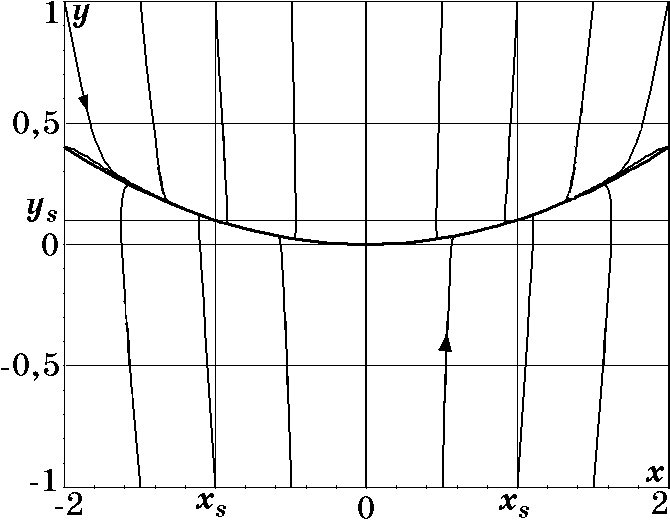
Рис. 2.1. Фазовый портрет системы (2.4) при $\lambda_2/\lambda_1=100$
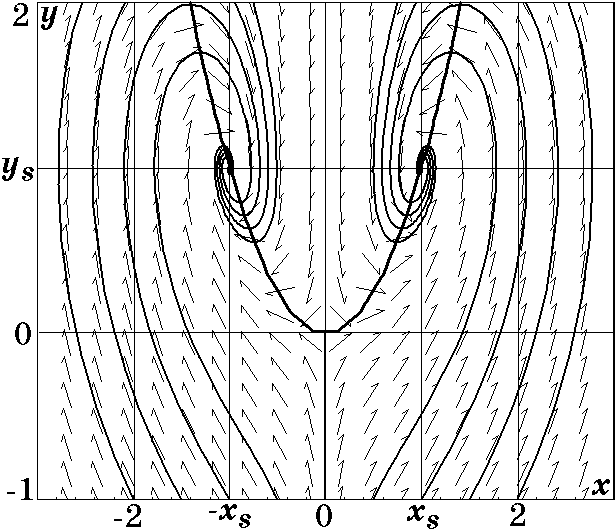
Рис. 2.2. Фазовый портрет системы (2.4) при $\lambda_2/\lambda_1=1$
Отметим, что эволюционными уравнениями вида (2.5) описывается обширный класс разнообразных физических (химических, биологических и др.) систем, в том числе и обладающих колебательными режимами движения [51, 43, 52, 54, 55].
Возникает фундаментальная проблема о целенаправленном применении идей и понятий синергетики — бифуркаций, параметров порядка, принципа подчинения и др. — для разработки регулярных методов исследования свойств самоорганизации нелинейных неуправляемых систем и, в особенности, придания такого рода свойств синтезируемым управляемым динамическим системам (2.3).
Как утверждают авторы монографии [55], “главная надежда нелинейной динамики состоит в том, что многие сложные системы могут быть просто описаны с помощью нескольких переменных — параметров порядка. Именно это в перспективе позволяет надеяться на понимание”. Однако для этого необходимо ответить на ключевой вопрос: каким образом появляются параметры порядка, позволяющие достаточно просто изучить поведение сложной нелинейной многомерной системы? В синергетике и нелинейной динамике этот вопрос в определенной мере разрешается на основе теории бифуркаций, теории инерциальных многообразий и механизма самоорганизации [51, 43, 52, 45, 53, 54]. Суть явления самоорганизации состоит в том, что в многомерных системах с течением времени происходит выделение параметров порядка — главных переменных, принадлежащих некоторому многообразию. Остальные переменные системы полностью подчиняются параметрам порядка. Это означает, что все траектории системы притягиваются и затем “оседают” на некоторой поверхности, нередко малой размерности, — многообразии в фазовом пространстве системы. Процедура выявления инерциальных (точнее “инерционных”) многообразий состоит в следующем [53].
$$
\begin{split}
\dot{\mathbf z}(t) &= \mathbf{F}_1\mathbf{(z,v)};\\
\dot{\mathbf v}(t) &= \mathbf{F}_2\mathbf{(z,v)}.
\end{split}\qquad
(2.8)$$
Предположим, что существует некоторое положительно инвариантное множество
$$
\mathbf v= \boldsymbol\Phi(\mathbf z)\qquad
(2.9)$$
такое, что на нем удовлетворяется второе уравнение системы (2.8), т.е.
$$
\frac d{dt}\boldsymbol\Phi(\mathbf z) -\mathbf{F}_2\mathbf{(z,v)}\equiv 0.
$$
При указанных условиях исходная $n$-мерная система (2.7) дифференциальных уравнений станет эквивалентной системе $\eta$ дифференциальных уравнений
$$
\dot{\mathbf z}(t) =\mathbf{F}_1\mathbf{(z},\boldsymbol\Phi(\mathbf z)) \qquad
(2.10)$$
и $n-\eta$ алгебраических уравнений (2.9). Уравнение (2.10) — это эволюционное уравнение, а $\mathbf z$ — параметр порядка. Для возникновения указанной ситуации на асимптотическом этапе движения исходной системы необходимо, чтобы многообразие (2.9) было притягивающим, т.е. асимптотически устойчивым. Именно такое асимптотически устойчивое инвариантное многообразие, содержащее аттрактор исходной системы, и называется инерциальным многообразием [53]. Важность описанного выше преобразования состоит в том, что движение декомпозированной динамической системы (2.10) на аттракторе обычно значительно проще по сравнению с общим случаем (2.7). Этот эффект объясняется тем, что при наличии инерциального многообразия можно опустить переходной процесс и рассматривать движение системы только на указанном многообразии. Тогда переменные, входящие в исходную систему, можно разделить на две группы: “существенные” — $\mathbf z(t)$, определяющие динамику, и “несущественные” — $\mathbf v(t)$, которые подчиняются первым и следуют за ними. Г. Хакеном переменные $\mathbf z(t)$ названы параметрами порядка [53].
Применительно к объекту (2.3) соотношение (2.6) является инвариантным многообразием типа (2.9), а $x(t)$ — параметром порядка. Движение на указанном многообразии описывается эволюционным уравнением (2.5) типа (2.10).
Теория инерциальных многообразий сыграла ключевую роль в развитии нелинейной динамики [53]. Однако до сих пор не предложены методы регулярного построения инерциальных многообразий для общего класса нелинейных дифференциальных уравнений, что, по-видимому, и невозможно. Сама процедура выявления таких многообразий обычно является результатом удачи и интуиции исследователя. Указанная проблема поиска инерциальных многообразий сходна с известной проблемой определения интегралов движения в классической механике, которой посвятили свои труды многие выдающиеся ученые XIX века. По поводу этой проблемы современный ученый М. Табор пишет: “...каким образом находить интегралы движения (если они существуют?). По мере того, как порядок уравнений возрастает, а их функциональный вид усложняется, эта задача становится очень сложной. Действительно, не существует сколь-нибудь систематической процедуры для ее решения — приходится полагаться на опыт, на удачу и, в безнадежных ситуациях, на провидение!” [41]. Это яркое высказывание в полной мере справедливо и для проблемы поиска инерциальных многообразий [53]. Следует, однако, отметить и существенную разницу в понимании указанных проблем. Дело в том, что интегралы движения в классической механике обычно имеют глубокое физическое содержание, связанное с законами сохранения энергии, импульса и т.д. Такого уровня понимания и отражения естественных свойств объектов, описываемых нелинейными дифференциальными уравнениями, теория инерциальных многообразий пока еще не достигла. А это обстоятельство имеет принципиальное значение для задач управления нелинейными многомерными объектами.
Параметры порядка в синергетике формируют макроскопическую структуру нелинейной системы. При этом поведение любой из координат $x_i(t)$ системы однозначно определяется параметрами порядка. Это означает, что движение системы в ее фазовом пространстве управляется параметрами порядка и подчинено именно им. В этом и состоит принцип подчинения в синергетике [52]. Суть подчинения состоит в том, что поведение системы определяется иерархией масштабов времени между “ускоренными” процессами изменения некоторых переменных и “медленными” процессами эволюции параметров порядка. Обычно число параметров порядка существенно меньше числа координат системы, т.е. в результате перехода к параметрам порядка существенно сокращается число степеней свободы системы, что приводит к значительному сжатию информации. Однако оказывается, что отдельные координаты $x_i(t)$, объединяясь в кооперативное движение, в свою очередь оказывают воздействие на сами параметры порядка. Это означает, что параметры порядка, с одной стороны, формируют движение отдельных координат системы, а с другой стороны, отдельные координаты в совокупности порождают параметры порядка. В синергетике описанное явление называют круговой причинностью. Объединяясь в параметры порядка, отдельные координаты системы стремятся найти консенсус [51, 52]. Иначе говоря, подчинение и поиск согласия являются двумя базовыми свойствами синергетического подхода в науке.
Те или иные “быстрые” и “медленные” переменные, находящиеся в иерархической подчиненности, можно интерпретировать как выходные координаты соответствующих “каскадов” нелинейных динамических систем. Указанные каскады в большинстве случаев имеют очевидный физический (химический, биологический и др.) смысл. По существу, свойство каскадности лежит в основе принципа подчиненности и теории параметров порядка в синергетике. Формирование параметров порядка обычно осуществляется на основе нелинейного (чаще мультипликативного) взаимодействия между “быстрыми” и “медленными” переменными системы. В целом, описываемые здесь процессы в своей совокупности и лежат в основе явления самоорганизации в нелинейной динамике и синергетике.
Следует отметить, что механизмы формирования параметров порядка во многом опираются на приближенный метод “малого” параметра в теории нелинейных дифференциальных уравнений, которому посвящена обширная литература [40, 56]. Этот метод основан, по существу, на идеологии асимптотического анализа и имеет во многом эвристический, нерегулярный характер. Отсюда следует необходимость разработки новых методов построения регулярных процедур формирования параметров порядка и, следовательно, направленной самоорганизации управляемых систем.
2.1.3. Направленная самоорганизация и притягивающие многообразия
Для того, чтобы показать возможность направленной самоорганизации в системе (2.3) со свойствами, определяемыми эволюционным уравнением (2.5), введем в рассмотрение следующую макропеременную:
$$
\psi_1(x,y)=x^2 -\lambda_2y.\qquad
(2.11)$$
Очевидно, что функция (2.11) на финишных этапах движения системы (2.3) должна быть, согласно (2.6), равной нулю. Это движение будет описываться эволюционным уравнением (2.5). Для того, чтобы удовлетворить условию $\psi_1(x,y)=0$ после выхода системы (2.3) на финишный этап движения, введем простейшее функциональное уравнение
$$
T_1\dot\psi_1(t) +\psi_1=0.
$$
Тогда, подставив сюда функцию $\psi_1(x,y)$ (2.11), с учетом исходных уравнений (2.3) найдем $u_1$ — обратную связь:
$$
u_1=\left(\frac{2\lambda_1}{\lambda_2}-1\right)x^2 -\frac 2{\lambda_2}x^2y +\lambda_2y +\frac 1{\lambda_2T_1}\psi_1.
$$
Подставив теперь $u_1$ в (2.3), находим уравнения сконструированной системы
$$
\begin{split}
\dot x(t) &=\lambda_1x -xy;\\
\dot y(t) &=\frac{2\lambda_1}{\lambda_2}x^2 -\frac 2{\lambda_2}x^2y +\frac 1{\lambda_2T_1}\psi_1.
\end{split}\qquad
(2.12)$$Система (2.12) имеет состояние $\psi_1=0$ как притягивающее многообразие — аттрактор. Для того чтобы это показать, найдем из первого и второго уравнений (2.12) величину $dt$ и представим систему (2.12) в следующей симметричной форме:
$$
dt=\frac{dx}{\lambda_1x -xy}=\frac{\lambda_2T_1dy}{2T_1(\lambda_1x -xy)x +\psi_1}.
$$Положив функцию $\psi_1=0$, после интегрирования находим частный интеграл $x^2=\lambda_2y$, который совпадает с выражением $\psi_1=0$ (2.11). В математике это означает, что система (2.12) имеет асимптотический аттрактор $\psi_1=0$, что и требовалось доказать.
Система (2.12), стартуя из произвольных начальных условий $x_0$, $y_0$ и, следовательно, $\psi_0=x_0^2 -\lambda_2y_0$, неизбежно через время $(4\div 5)T_1$ должна выйти на аттрактор $\psi_1=0$ — притягивающее многообразие. Другими словами, ее движение на финишном этапе будет обязательно протекать по многообразию $\psi_1=0$ (2.11) или в его окрестности. Это движение описывается уравнением
$$
\dot x_{\psi}(t) =\lambda_1 x_{\psi} -\frac 1{\lambda_2}x_{\psi}^3.\qquad
(2.13)$$Дифференциальное уравнение (2.13) описывает движение системы (2.12) на аттракторе $\psi_1(x,y)=0$, т.е. на ее финишном этапе.
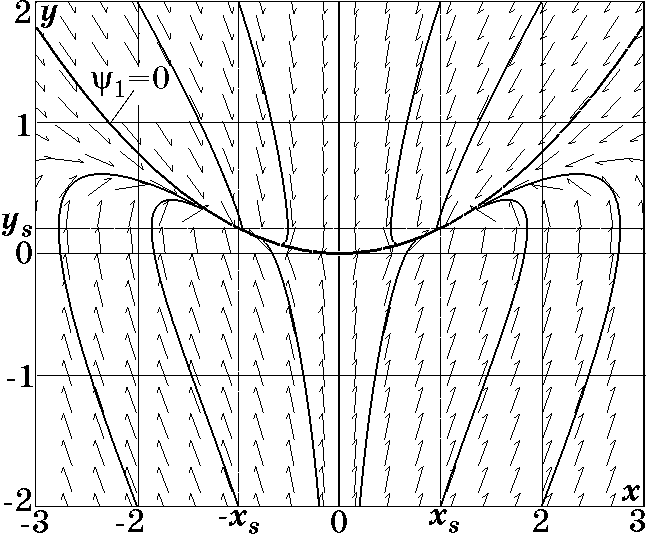
Рис. 2.3. Фазовый портрет системы (2.12) при $\lambda_2/\lambda_1=100$ и $T_1=10/\lambda_2$
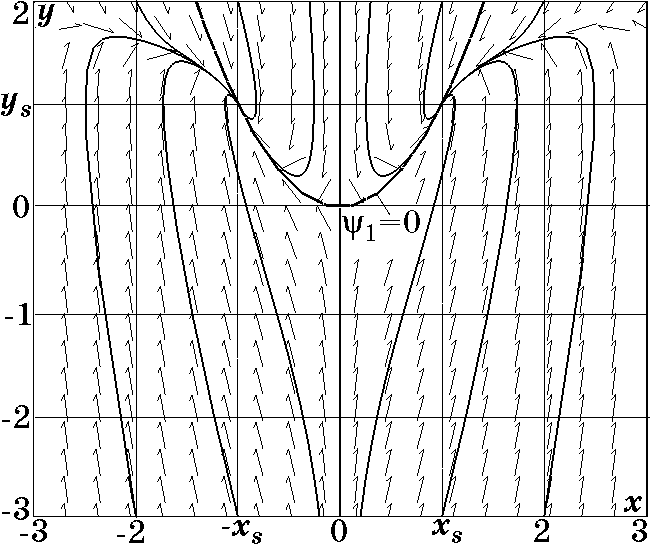
Рис. 2.4. Фазовый портрет системы (2.12) при $\lambda_2/\lambda_1=1$ и $T_1=0,5/\lambda_2$
На рис. 2.3 изображен фазовый портрет системы (2.12) при $\lambda_2/\lambda_1=100$ и $T_1=10/\lambda_2$, из которого видно, что траектории сначала устремляются к аттрактору $\psi_1=0$ (2.11), а затем движутся вдоль него к стационарным точкам $x_s=\pm\sqrt{\lambda_1\lambda_2}$, $y_s=\lambda_1$, т.е. имеет место кооперативный процесс. Аналогично, на рис. 2.4 изображен фазовый портрет системы (2.12) при $\lambda_2/\lambda_1=1$ и $T_1=0,5/\lambda_2$, из которого следует, что, в отличие от случая $u_1=0$ (рис. 2.2), траектории сближаются с аттрактором $\psi_1=0$ (2.11), а затем движутся вдоль него к стационарным точкам $x_s=\pm\sqrt{\lambda_1\lambda_2}$, $y_s=\lambda_1$, т.е. по-прежнему возникают кооперативные явления.
Система (2.4) в установившемся режиме может равновероятно находиться в одном из двух возможных состояний: $x_s=\pm\sqrt{\lambda_1\lambda_2}$, $y_s=\lambda_1$. В системе (2.12) также устанавливаются эти состояния, при этом функция $u_{1s}=0$. В целом, это означает полную идентичность поведения систем (2.4) и (2.12) на этапе самоорганизации.
Итак, установлено, что поведение сконструированной системы (2.12) на аттракторе $\psi_1(x,y)=0$ (2.11) представляется уравнением (2.13). Замечательно, что это уравнение точно совпадает с широко известным в синергетике и теории самоорганизации эволюционным уравнением (2.5), описывающим движение системы (2.4) на финишном этапе и обладающим бифуркацией типа “вилка”. Это означает, что система (2.4) при $\lambda_2\gg|\lambda_1|$ (рис. 2.1)) и сконструированная система (2.12) (рис. 2.3, рис. 2.4) обладают одинаковыми кооперативными свойствами относительно “параметра порядка” $x$, в том числе и свойством самоорганизации.
Возникает интересный вопрос, чем же отличаются системы (2.4) и (2.12)? Дело в том, что возможность появления кооперативного, когерентного движения в системе (2.4), описываемого уравнением (2.5), существенно зависит от соотношения параметров $\lambda_1$ и $\lambda_2$. Иначе говоря, адиабатическое приближение (2.6) тем точнее и тем раньше наступает, чем сильнее соотношение $\lambda_2\gg|\lambda_1|$. Об этом свидетельствуют фазовые портреты, изображенные на рис. 2.1 и рис. 2.2 при $\lambda_2/\lambda_1=100$ и $\lambda_2/\lambda_1=1$ соответственно. В первом случае, когда $\lambda_2\gg|\lambda_1|$, существенно проявляются кооперативные процессы, а во втором, когда $\lambda_2\cong\lambda_1$, они заметно ослабляются или вовсе отсутствуют.
В математике такое приближение основано на методах асимптотической декомпозиции — расщепления системы на подсистемы меньшей размерности. Эти методы [40, 56] базируются на идее “малого параметра”, выявление которого в исследуемой системе представляет собой, как правило, существенно неформализуемую процедуру. Такого рода приближение можно назвать параметрической декомпозицией. По существу, к параметрическим во многом относятся известные методы синергетики и теории самоорганизации, сама терминология которых об этом свидетельствует — “управляющие параметры”, “параметры порядка” и др. В синергетике доминирует “параметрическое” управление, когда через “управляющие” параметры, принцип подчинения и “параметры порядка” возникает самоорганизация. Справедливости ради, следует отметить, что на этом “параметрическом” пути синергетика добилась в последнее время весьма впечатляющих результатов [51, 43, 52, 45, 53, 54].
Существенно расширяет возможности для конструирования нового класса самоорганизующихся систем синергетический метод синтеза, основанный на идее введения в фазовое пространство синтезируемых систем некоторых желаемых аттракторов. Здесь задача состоит в том, чтобы ввести в систему такую структуру — аттрактор, которая обеспечивает движение системы на финишных этапах в соответствии с типичными эволюционными уравнениями синергетики [52]. При параметрическом подходе процесс выхода в окрестность точки бифуркации ($\lambda_{1c}=0$) и затем на ту или иную асимптотическую ветвь решения, например уравнения (2.5), во многом зависит от выполнения параметрических соотношений, в частности вида $\lambda_2\gg|\lambda_1|$ (рис. 2.1 и рис. 2.2). При структурном же подходе указанный процесс выхода на соответствующую структуру (2.5) фактически неизбежен (рис. 2.3) и рис. 2.4), а время выхода определяется параметром $T_1$, выбираемым конструктором системы. В этом случае закон управления $u_1$, условно говоря, как бы “разрывает” жесткую связку между параметрами ($\lambda_1$ и $\lambda_2$) системы.
Итак, в системе может быть направленно сформирована желаемая структура — аттрактор, на которой возникает процесс самоорганизации. Такое явление называется направленной (целеподобной) самоорганизацией.
Важно подчеркнуть, что в системе (2.3) за счет выбора соответствующих обратных связей $u(x,y)$ можно обеспечить и другие виды бифуркации, т.е. иные типы самоорганизации. В синергетике, помимо описанной выше бифуркации типа “вилки” (2.5), распространена также транскритическая бифуркация [53, 45, 53], уравнение которой относительно параметра порядка имеет вид
$$
\dot x(t)=\lambda_1x-\beta_1x^2\qquad
(2.14)$$и представляет собой широко известное в экологии логистическое уравнение, которое, в свою очередь, является частным случаем уравнения Бернулли.
Транскритическая бифуркация невозможна в системе (2.3) при любом сочетании параметров $\lambda_1$ и $\lambda_2$ в случае $u=0$. Однако, за счет выбора соответствующей функции $u(x,y)$, указанную бифуркацию можно элементарно обеспечить. Для этого следует выбрать простейшую макропеременную
$$
\psi_2=\beta_1x-y,
$$подставив которую в уравнение
$$T_2\dot\psi(t) +\psi_2=0,
$$можно получить с учетом уравнений (2.3) следующую обратную связь:
$$
u_2=\lambda_1x -xy +\lambda_2y -x^2 +\frac 1{T_2}\psi_2.
$$Подставив $\psi_2=0$, т. е. $y=\beta_1x$, в первое уравнение системы (2.3), получим уравнение
$$
\dot x_{\psi}(t) =\lambda_1x_{\psi} -\beta_1x_{\psi}^2,
$$которое описывает движение замкнутой системы на многообразии $\psi_2=0$ и точно совпадает с (2.14). Это означает, что в системе (2.3) с обратной связью на финишном этапе через время $(4\div 5)T_2$ возникнет движение на аттракторе $\psi_2=0$ уже с транскритической бифуркацией (2.14). На рис. 2.5 изображен фазовый портрет системы (2.1) с обратной связью $u_2$, из которого видно, что траектории сначала устремляются к аттрактору $\psi_2=0$, а затем движутся вдоль него к стационарной точке $x_s=\lambda_1/\beta_1$, $y_s=\lambda_1$, т.е. возникает кооперативный процесс с транскритической бифуркацией.
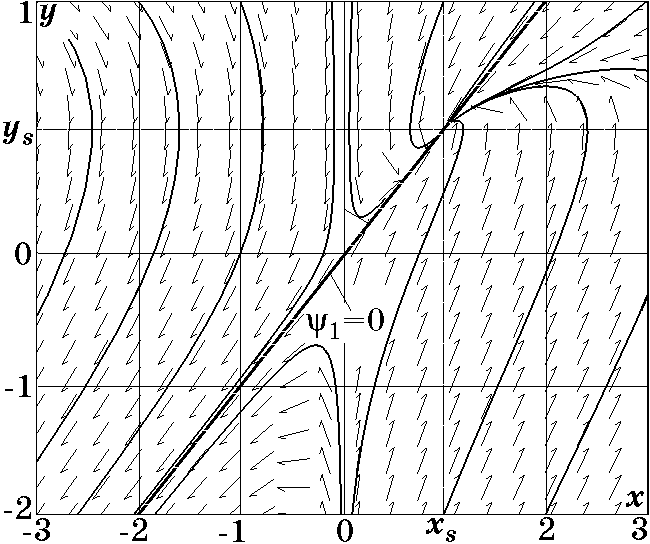
Рис. 2.5. Фазовый портрет системы (2.1) с обратной связью $u_2$
Если ввести макропеременную
$$
\psi_3=\lambda_3-\frac{\mu -x^2}{x} -y
$$и подставить ее в функциональное уравнение
$$T_3\dot\psi(t) +\psi_3=0,
$$то тогда в силу исходных уравнений (2.3) найдем следующую обратную связь:
$$
u_3=\lambda_2y -x^2 -\frac{\mu -x^2}{x^2}(\lambda_1 x -xy) +\frac 1{T_3}\psi_3.
$$Подставив теперь эту обратную связь в (2.3), получим уравнения замкнутой системы:
$$
\begin{split}
\dot x(t) &= \lambda_1 x - xy;\\
\dot y(t) &= -\frac{\mu -x^2}{x^2}(\lambda_1 +xy) +\frac 1{T_3}\psi_3.
\end{split}\qquad
(2.15)$$Очевидно, что полученная система (2.15) имеет притягивающее инвариантное многообразие $\psi_3=0$, к которому устремляются все ее фазовые траектории. Движение системы (2.15) вдоль этого многообразия описывается дифференциальным уравнением
$$
\dot x_\psi (t) =(\lambda_1 -\lambda_3)x_\psi +\mu -x_\psi^2.
$$Из этого уравнения при $\lambda_3>\lambda_{1\max}$ и $\mu=0$ получаем эволюционное уравнение вида (2.14) с транскритической бифуркацией, а при $\lambda_1=\lambda_3$ из него следует уравнение вида
$$
\dot x_\psi (t) =\mu -x_\psi^2.
$$Это типичное эволюционное уравнение синергетики с бифуркацией типа “седло—узел”, часто встречающейся в различных физических приложениях [53].
Итак, введение в систему (2.3), изначально используемую в работах Г. Хакена [52] для демонстрации идеи самоорганизации в синергетике, соответствующих обратных связей позволяет сформировать желаемые типы бифуркаций и тем самым реализовать направленную самоорганизацию системы.
Введение обратных связей $u(x,y)$ и формирование с их помощью процессов направленной самоорганизации позволяет перейти от приближенной параметрической (разнотемповой) декомпозиции систем ($\lambda_2\gg|\lambda_1|$) при стандартных процедурах теории самоорганизации [51, 43, 52, 45, 53, 54] к точной динамической декомпозиции в методах СТУ [57]. При этом движение системы на финишных этапах будет описываться совпадающими эволюционными уравнениями. Разумеется, что функцию $u(x,y)$ в уравнениях (2.3) вовсе не обязательно понимать как управление, она, например, может отражать некоторую дополнительную (изменяемую) часть конструкции системы соответствующей природы. Такие изменяемые части обычно реализуются путем введения соответствующих обратных связей, что и составляет основное содержание теории управления.
Обобщим теперь изложенный здесь синергетический подход к синтезу систем, опираясь на идеологию единства процессов направленной самоорганизации и управления.